Theory

In this chapter the theory underlying the TROVE program will be described. Since the original TROVE paper many new features have been added to the code and described in publications as used. Here all of the theoretical framework for the main aspects of TROVE shall be described in one place.

The aim of this chapter is not to derive and explain every technical aspect of TROVE per say but to give users knowledge of the underlying concepts of TROVE. This is especially useful for those using it as a ‘black box’ (and for PhD Vivas!). For full technical details of derivations and theoretical concepts, the reader should consult the references as given and the TROVE source code.

The TROVE Approach

The Schrödinger equation for a molecule within the Born-Oppenheimer (BO) approximation can be written in laboratory-fixed XYZ Cartesian coordinates as

\left(-\frac{\ \hbar^2}{2} \sum_{i=1}^N \frac{1}{m_i} \nabla^2_i + V \right) \Psi_{trv} = E_{trv} \Psi_{trv}

where nucleus i has mass m_i and coordinates (R_{iX},R_{iY},R_{iZ}). \nabla^2_i = \partial ^2 / \partial R_{iX}^2 + \partial ^2 / \partial R_{iY}^2 + \partial ^2 / \partial R_{iZ}^2 is the kinetic energy for each nucleus and V is the potential energy, which is equal to the electronic energy within the BO approximation (and absence of electric and magnetic fields). \Psi_{trv} and E_{trv} are the wavefunction and energy respectively.

Although this equation has a simple mathematical form, it is not suited for actual solution. The label trv on the energies and wavefunction stands for translation, rotation and vibration. In this coordinate system these motions are all coupled. Translational motion can be exactly separated from rotation and vibration (indeed, for spectroscopy we are usually not interested in the overall translation of a molecule through space). Rotational and vibrational motion are often fairy weakly coupled and coordinates can be chosen to exploit that fact. Maximal separation of all of these motion makes the solution of the nuclear Schrödinger equation simpler.

To carry out this decoupling, a more suitable coordinate system is required. This usually involves introducing a molecule-fixed (or body-fixed) axis system, xyz with the origin at the molecule’s centre of mass. Thus the nuclear locations are some vector from the centre of mass rather than from some origin in space in the XYZ system. If the molecule is rotating then the molecule-fixed axis will rotate with the molecule.

Defining a molecule-fixed axis system immediately introduces a problem however due to the variety of shapes and sizes of molecules. For each molecule type (e.g. trigonal pyramidal, tetrahedral, etc) there are different choices of coordinate system which lead to different kinetic energy operators (and different computer programs for their solution). Normal coordinates are an exception and can be defined in a general manner but are best suited for small amplitude vibrations near a molecule’s equilibrium structure.

TROVE takes a different approach by numerically constructing the kinetic energy operator for a given molecule and axis system. This is achieved using a Taylor expansion of the Hamiltonian in terms of internal coordinates of the molecule. This allows TROVE to be used for a wide variety of molecules as seen in chapter Molecules. The actual construction of the Hamiltonian can be used in a rather black box manner, with the user only needing to define coordinate transforms and so on (see chapter New molecule ).

A particular strength of TROVE is the ability to calculate eigenfunctions and eigenvalues of high angular momentum quantum number J by minimising the coupling of the vibrational and rotational motion. Access to high J is crucial for the simulation of molecular spectra, especially at high temperatures where lots of states are populated.

Numerical Construction of Kinetic Energy Operator

To construct the kinetic energy operator TROVE expresses the Hamiltonian in equation schrodiger_lab_cart in terms of the generalised coordinates

(1)\Xi = \left(R_X^{CM},R_Y^{CM},R_Z^{CM},\theta,\phi,\chi,\xi_1,\xi_2 \cdots ,\xi_{3N-6} \right)

where R_F^{CM} = \sum_{i=1}^N m_iR_{iF} / \sum_{j=1}^N m_j (F=X,Y,Z) is the F-coordinate of the nuclear centre of mass; these three coordinates describe translation of the molecule through space. The three Euler angles (\theta,\phi,\chi) define the orientation of the xyz molecule-fixed axis relative to lab-fixed XYZ and thus define overall rotation (for a description of Euler angles see Bunker and Jensen [98BuJe] or Zare’s book on angular momentum [88Zare]). The \xi_n coordinates described vibration. There are 3N - 6 of these for a non-linear molecule and they can be defined in whatever manner is convenient (see below).

The transformed kinetic energy operator \hat{T} is essentially a quadratic form in the generalised momenta (recall that -\frac{\hbar^2}{2m} \frac{\partial^2 }{ \partial x^2 } = \frac{1}{2m} \left( -i \hbar \frac{\partial}{\partial x} \right)^2 = \frac{\hat{p}^2}{2m} )

(2)\hat{\Pi} = \left(\hat{P}_X^{CM}, \hat{P}_Y^{CM},\hat{P}_Z^{CM},\hat{J}_x,\hat{J}_y,\hat{J}_z,\hat{p}_1,\hat{p}_2, \cdots ,\hat{p}_{3N-6} \right)

where \hat{P}_F^{CM} (F=X,Y,Z) is the momentum conjugate to (associated with) the translation motion of the centre of mass coordinate R_F^{CM}, (\hat{J}_x, \hat{J}_y, \hat{J}_z) are the xyz components of the total angular momentum and \hat{p}_n = -i \hbar \partial / \partial \xi_n (n=1, \cdots , 3N-6) is the momentum conjugate to \xi_n.

It is possible to write \hat{T} in these generalised momenta as

(3)\begin{split} \hat{T} &= \frac{1}{2} \sum_{F=X,Y,Z} \hat{P}_F^{CM} G_{FF} \hat{P}_F^{CM} \\ &+ \frac{1}{2} \sum_{\alpha=x,y,z} \sum_{\alpha'=x,y,z} \hat{J}_{\alpha} G_{\alpha,\alpha'}(\xi) \hat{J}_{\alpha'} \\ &-\frac{i \hbar}{2} \sum_{\alpha=x,y,z} \sum_{n=1}^{3N-6} \left[\hat{J}_{\alpha} G_{\alpha,n}(\xi) \frac{\partial}{\partial \xi_n} \right. \\ & \left. + \frac{\partial}{\partial \xi_n} G_{\alpha,n}(\xi) \hat{J}_{\alpha} \right] \\ &-\frac{\hbar^2}{2} \sum_{n=1}^{3N-6} \sum_{n'=1}^{3N-6} \frac{\partial}{\partial \xi_n} G_{n,n'}(\xi) \frac{\partial}{\partial \xi_{n'}} + U(\xi). \end{split}

This equation expresses the fact that the kinetic energy operator \hat{T} can be expressed in terms of an expansion of the generalised momenta with suitable expansion coefficients G_{\lambda,\lambda'}. The first term is the translation kinetic energy of the centre of mass for which G_{XX} = G_{YY} = G_{ZZ} = 1 / \sum_{j=1}^N m_j. This term is exactly separable from the other terms as expected. The second term is the kinetic energy of rotation, third term is the coupling between rotational and vibrational motion, fourth term is the kinetic energy of vibrational motion and the final term is the pseudopotential term. For these terms all of the G_{\lambda,\lambda'} depend on the complete set of vibrational coordinates \xi. We can write equation (3) in the compact form

(4)\hat{T} = \frac{1}{2} \sum_{\lambda=1}^{3N} \sum_{\lambda'=1}^{3N} \hat{\Pi}_{\lambda} G_{\lambda,\lambda'}(\xi)\hat{\Pi}_{\lambda'} + U(\xi)

where \Pi_{\lambda} is an element of \hat{\Pi} of equation (2).

The vibrational coordinates \xi_n can be any coordinates which represent the internal degrees of freedom and unambiguously define the instantaneous relative positions of the nuclei. Examples are internal displacement coordinates (i.e. displacement of bond lengths, angles and dihedral angles from equilibrium values), linearised interal coordinates (see below) and symmetric combinations of these. This ability to choose which coordinates to use is the power of this approach which makes it applicable to a wide variety of molecules.

To utilise equation (3) the expansion terms G_{\lambda,\lambda'}(\xi), pseudopotential term U(\xi) and the Born-Oppenheimer potential energy function V must be expressed in terms of \xi_n. This is done by expressing these quantities as a series expansion in terms of the \xi themselves or functions of them

(5)g_n = g_n(\xi_n).

Thus, we can write

and

where G_{l_1,l_2,l_3,\cdots}^{\lambda,\lambda'} and U_{l_1,l_2,l_3,\cdots}^{\lambda,\lambda'} are constant expansion coefficients. Similarly the potential V is expressed as

where V_{l_1,l_2,l_3} are constant expansion coefficients in terms of convenient expansion functions

(6)f_n = f_n(\xi_n).

For example f_n = 1 - \exp(-a \xi_n) (Morse type) or f_n = \cos(\xi_n). Typically Morse or Harmonic functions are used for bond stretches and \xi_n is used itself for bends.

The method of actually finding the expansion coefficients introduced above will now be discussed. This is arguably the most technical part of the TROVE approach and could be skipped on first (or even second!) reading. It is based on a paper by Sorensen [Sorensen].

To go from the expression for the kinetic energy in equation schrodiger_lab_cart to that in equation (3) we start by noting that \hat{T} in the former equation can be expressed as

(7)\hat{T} = -\frac{\hbar^2}{2} \sum_{i=1}^N \frac{1}{m_i} \nabla^2_i = \sum_{X,Y,Z} \sum_{i=1}^{N}\frac{\hat{P}^2_{iF}}{2m_i} = \sum_{i=1}^N \frac{\hat{\mathbf{P}}_i^2}{2m_i}

where the momentum vector \hat{\mathbf{P}}_{iF} has the XYZ coordinates (\hat{P}_{iX}, \hat{P}_{iY}, \hat{P}_{iZ}). The chain-rule transformation in Hermitian form is defined as

with

This relation states that the momentum in the XYZ lab-fixed coordinate system \hat{P}_{iF} can be expressed in terms of the generalised momenta \hat{\Pi} with the derivative of the generalised coordinates \Xi with respect to a given lab-fixed coordinate R_{iF} linking them. The Jacobian-matrix elements s_{\lambda,iF} (F = X,Y,Z) define vectors and so the vector from of equation chain_hermit is

(8)\hat{\mathbf{P}}_i = \frac{1}{2} \sum_{\lambda = 1}^{3N} \left(\mathbf{s}_{\lambda,i} \hat{\Pi}_{\lambda} +\hat{\Pi}_{\lambda} \mathbf{s}_{\lambda,i}\right).

When equation (8) is inserted into equation (7) the following equations for the G_{\lambda,\lambda'} coefficients and pseudopotential term U are given

(9)G_{\lambda,\lambda'} = \sum_{i=1}^N \frac{\mathbf{s}_{\lambda,i} \mathbf{s}_{\lambda',i}}{m_i}

(10)U = \sum_{\lambda=1}^{3N} \sum_{\lambda'=1}^{3N} \sum_{i=1}^N \left\{ \frac{1}{8m_i} \left[\hat{\Pi}_{\lambda},\mathbf{s}_{\lambda,i} \right] \cdot\left[\hat{\Pi}_{\lambda'},\mathbf{s}_{\lambda',i} \right]+ \frac{1}{4 m_i} \mathbf{s}_{\lambda,i} \cdot \left[\hat{\Pi}_{\lambda},\left[\hat{\Pi}_{\lambda'},\mathbf{s}_{\lambda',i}\right] \right] \right \}

where the square brackets indicate the communicator of the quantities in them.

To make progress the quantity t_{iF,\lambda} is introduced with the definition

(11)t_{iF,\lambda} = \frac{\partial R_{iF}}{\partial \Xi_{\lambda}}.

From the application of the chain rule the following relation is found

(12)\sum_{i=1}^{N} \sum_{F=X,Y,Z} \frac{\partial \Xi_{\lambda} }{\partial R_{iF} } \frac{\partial R_{iF}}{\partial \Xi_{\lambda'}}= \mathbf{s}_{\lambda,i}\cdot \mathbf{t}_{i,\lambda'} = \delta_{\lambda,\lambda'}

where the vector \mathbf{t}_{i,\lambda'} has been introduced. If the \mathbf{t}_{i,\lambda'} vectors are known then we can solve this equation to obtain the \mathbf{s}_{i,\lambda'} vectors.

At this point further technical details of how to solve equation (12) will not be given and instead the interested reader is referred to the TROVE paper [TROVE] for more information. Instead a qualitative description will be given.

Sorensen [Sorensen] showed what values the various components of the \mathbf{t}_{i,\lambda'} vectors have, consistent with Eckart conditions, which achieve optimum separation of rotational and vibrational motion. Equation (12) can then be solved numerically. Components of the \mathbf{s}_{\lambda,i} and \mathbf{t}_{i,\lambda'} are expanded as a power series in g_n({\xi_n}) (from equation (5) above) to a given order (this is what the integer after verb|kinetic| refers to in the TROVE input file). When these power series are substituted into equation (12) and coefficients up to a given order are collected, a system of linear equations is obtained of form \mathbf{T}\mathbf{x} = \mathbf{b}. The systems of equations can be set up and solved numerically by making use of the fact that values of \mathbf{t}_{i,\lambda'} are known.

The result of all this is that equations for G_{\lambda,\lambda'} and U given in equations (9) and (10) are expressed in terms of products of g_n(\xi_n) raised to powers and multiplied by expansion coefficients which are found from the linear equations described. This ultimately means that we can write \hat{T} in terms of molecule-fixed xyz coordinates as in equation :eq:`generalT:. The entire procedure (although complicated) is a numerical one and thus does not require any analytic algebra to define the kinetic energy operator for a given molecular shape. This is what makes TROVE general.

Vibrational Coordinates

The procedure described in the previous section for the numerical construction of the kinetic energy operator is general and can be used with any choice of suitable vibrational coordinates \xi_n as long as t_{i \alpha,\mu} can be provided. There are three basic types of coordinates used by TROVE: linearized coordinates, geometrically defined coordinates and coordinates for non-rigid molecules with large amplitude vibrations. Of these, linearized coordinates tend to be used the most but geometrically defined coordinates have been used more recently due to a better implementation for them [15YaYu]. Each type of coordinate shall be described in the next subsections.

Linearized Coordinates

The linearized coordinates are introduced in terms of the Cartesian displacements d_{i \alpha} (where i = 1 to N nuclei and \alpha = x,y,z) of the nuclei from their equilibrium positions a_{i \alpha} in the xyz molecule-fixed axis system

(13)R^{MS}_{i \alpha} = a_{i \alpha} + d_{i \alpha}.

In general the 3N - 6 internal displacement coordinates \xi_n are non-linear functions of the displacements d_{i,\alpha} since, for example a bond stretch or bend will not usually lie along an axis. A set of 3N-6 linearized coordinates \xi_n \equiv \xi_n^l are defined to be linear combinations of d_{i \alpha} and to coincide with the 3N-6 coordinates \xi_n in the linear approximation

(14)\xi_n^l = \sum_{i=1}^N \sum_{\alpha=x,y,z} B_{n,i \alpha} d_{i \alpha}

where B_{n,i \alpha} = \partial \xi_n / \partial d_{i \alpha} are derived at equilibrium. The B_{n,i \alpha} can be obtained from geometrical considerations (for example using trigonometry, etc).

The xyz coordinate system has its origin at the molecule’s centre of mass and so the constant equilibrium coordinates a_{i \alpha} in equation (13) satisfy

(15)\sum_{i=1}^N m_i a_{i \alpha} = 0.

The a_{i \alpha} are easy to determine from the molecule’s equilibrium geometry but they can be obtained numerically from the Z-matrix. This gives an arbitrary molecule fixed axis x'y'z' which is transformed to the principle axis system xyz by means of a diagonalization of the inertial matrix.

For linear coordinates the expansions needed for determining the kinetic energy operator are linear. This makes them amenable to be numerically solved. The details are given in the TROVE publication [TROVE]. The simple form of the kinetic energy operator is an advantage of these coordinates.

Geometrically Defined Coordinates

Although linearized coordinates give a simple form for the kinetic energy operator they are not as good for expanding the potential energy. Geometrically defined coordinates have the advantage that when used, lower expansion orders are required for an accurate representation of the potential. Geometrically defined coordinates are any convenient coordinates used to unambiguously define a molecule’s geometry for example, the bond lengths and angles from a Z-matrix.

A disadvantage of these coordinates is that the kinetic energy operator is harder to derive with the expansion being non-linear. The original TROVE publication describes how this can be carried out numerically using ‘quadruple precision’ in the program to calculate numerical derivatives accurately.

A new way to obtain the expansion of the Hamiltonian was developed by Andrey Yachmenev by using ‘automatic differentiation’. This is a computational method of obtaining derivatives of functions with the accuracy of symbolic algebra but carried out in a numerical manner. The technical details of expanding the Hamiltonian and making use of the Eckart frame are discussed in detail in the publication [15YaYu]. Examples comparing linear and geometrically defined (or ‘curvilinear’) coordinates are also presented.

Coordinates for Large Amplitude Vibrations

If the kinetic and potential energy operators cannot be expanded in a Taylor series then a different approach is required. This is the case for molecules with a large amplitude degree of freedom for example inversion in ammonia or torsional motion in ethane. This degree of freedom will be labelled as coordinate \rho.

The method TROVE uses to handle this case is the Hougen-Bunker-Johns or HBJ approach. A grid of equidistant values along \rho is introduced. Each point of this grid is called a reference configuration. The remaining 3N-7 small amplitude vibrational coordinates are then defined as displacements from this configuration. At each grid point along \rho all relevant functions are expanded in terms of the small amplitude coordinates \xi_n. The steps given above for expanding the kinetic energy operator in either linearized or geometrically defined coordinates are carried out at each grid point along \rho. The details are given in the TROVE paper [TROVE].

Expansion of the Potential Energy Function

The potential energy function for a molecule is typically expressed in some suitable coordinates, ideally in a symmetrised form. This function is required as an input to TROVE (see Chapter New molecules) but for computational efficiency, TROVE re-expresses the potential in terms of the chosen coordinates \xi (:eq.v_exp_func:)

(16)V(\xi_n) = \sum_{l_1 = 0}^L \sum_{l_2 = 0}^{(L-l_1)} \cdots \sum_{l_{(3N-6)-1}=0}^{ (L-l_1 \cdots l_{(3N-6)-2})} V_{l_1 l_2 \cdots l_{(3N-6)}}^L \prod_i f_n^{l_i} = \sum_{L=0}^{N_{pot}} \sum_{L[l]} V_{L[l]}(f_n)^{L[l]}.

This is a sum of products of the coordinates (or functions of the coordinates) used raised to powers. This means that all integrals involving the potential will be separable into products of one-dimensional integrals. The expansion coefficients are obtained from the input potential using finite difference methods. This step also requires use of quadruple precision numbers in the program to avoid the accumulation of round off errors. The order to expand the potential to, N_{pot} is controlled by the verb|potential| keyword in the TROVE input file.

Vibrational Basis Functions and Matrix Elements

TROVE solves the Schrödinger equation using the variational method. This requires a suitable choice of basis functions for the method to be efficient. TROVE builds basis functions, starting from one-dimensional basis sets for each vibrational motion. These are then combined and truncated to build up a basis for the full dimensionality of the molecule. The details of this process are given here.

From the previous sections the rotation-vibration Hamiltonian expanded in terms of molecule-fixed xyz coordinates is given (in notation introduced in equation :eq:`V_expand:) as

(17)\hat{H}_{rv} = \frac{1}{2} \sum_{L \geq 0} \sum_{L[l]} \sum_{\lambda,\lambda'} \hat{\Pi}_{\lambda} G_{L[l]}^{\lambda,\lambda'}(g)^{L[l]}\hat{\Pi}_{\lambda'} + \sum_{L \geq 0} \sum_{L[l]} U_{L[l]}(g)^{L[l]}+ \sum_{L \geq 0} \sum_{L[l]} V_{L[l]} (f)^{L[l]}

with g_n(\xi_n) and f_n(\xi_n) defined in equations (5) and (6). TROVE uses vibrational basis set functions |\nu \rangle constructed as products of 1D basis functions

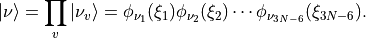
(18)|\nu \rangle = \prod_{v} | \nu_v \rangle = \phi_{\nu_1}(\xi_1)\phi_{\nu_2}(\xi_2)\cdots \phi_{\nu_{3N-6}}(\xi_{3N-6}).

The 1D basis functions implemented in TROVE are either analytically defined harmonic-oscillator or Morse-oscillator functions or are numerical solutions to the 1D Schrödinger equations for each vibrational coordinate obtained using Numerov-Cooley integration. These numerical solutions are obtained by solving

(19)\hat{H}_n^{(1D)} | \nu_n \rangle = E_{\nu_n} | \nu_n \rangle

for the Hamiltonian

(20)\hat{H}_n = -\frac{\hbar^2}{2} \frac{\partial}{\partial \xi_n} G_{n,n}^{(1D)}(\xi_n) \frac{\partial}{\partial \xi_n}+ V^{(1D)}(\xi_n) + U^{(1D)}(\xi_n)`

where the other 3N-7 coordinates are constrained to their equilibrium values to give G_{n,n}^{(1D)}(\xi_n), V^{(1D)}(\xi_n) and U^{(1D)}(\xi_n).

The vibrational matrix elements of the Hamiltonian in equation (17) can all be expressed in terms of one-dimensional integrals of each \xi_n coordinate as

(21)\begin{split} V_{\nu_n,\nu'_n}^l(n) &= \left< \nu_n | f_n^l(\xi_n) | \nu'_n \right>, \\ &T^{(0),l}_{\nu_n,\nu'_n}(n) = \left< \nu_n | g_n^l(\xi_n) | \nu'_n \right>, \\ &T^{(1),l}_{\nu_n,\nu'_n}(n) = \left< \nu_n | g_n^l(\xi_n) \frac{\partial}{\partial \xi_n} | \nu'_n \right>, \\ &T^{(2),l}_{\nu_n,\nu'_n}(n) = \left< \nu_n | \frac{\partial}{\partial \xi_n} g_n^l(\xi_n) \frac{\partial}{\partial \xi_n} \nu'_n \right>. \end{split}

The integrals are computed in TROVE using Simpson’s rule if numerically obtained basis functions are used or analytically if Harmonic or Morse oscillator functions are used. First derivatives are computed numerically using finite difference methods. Vibrational matrix elements of the Hamiltonian in (17) are then given by products of the matrix elements given in equations (21). If the HBJ approach is required then these 1D matrix elements are computed for each grid point along \rho (see the TROVE paper [TROVE]).

Rotational Basis Functions

TROVE uses linear combinations of rigid-rotor functions given as linear combinations |J,K,m,\pm \rangle

(22)|J,0,m,+ \rangle = |J,0,m \rangle, |J,K,m,\pm \rangle = \frac{p(J,K,\pm)}{\sqrt{2}} \left(|J,K,m\rangle \pm |J,-K,m\rangle \right)

where J is the total angular momentum (specified by the verb|0,’JKtau’, Jrot n| part of the TROVE input file in the basis block), K and m are projections of J onto a certain axis. \frac{p(J,K,\pm)}{\sqrt{2}} is a phase factor chosen to make the matrix representations of the kinetic energy operator real.

Descriptions of these functions are given in introductory textbooks to quantum mechanics and in detail in Bunker and Jensen’s book [98BuJe]. Matrix elements of these functions with the \hat{J}_{\alpha} operators are analytical.

The complete basis set which to be used in TROVE was a combination of these functions with the vibrational functions

(23)|\nu,J,K,m,\pm \rangle = \prod_{v} |\nu _v \rangle \times |J,K,m,\pm \rangle.

This form of basis set can still be used in TROVE but it is much efficient to use the J=0 method discussed below.

Diagonalisation of the Hamiltonian

The previous sections of this chapter have described: how the rotational-vibrational Hamiltonian is expanded in terms of internal coordinates of the molecule, the vibrational basis functions used in TROVE and how matrix elements of them are computed and the rotational basis functions used in TROVE. With all of this in place, the final computation required to obtain the rotational-vibrational energies and eigenfunctions is to diagonalise the Hamiltonian matrix.

The Schrödinger equation in matrix form is written as

(24)\mathbf{H}\mathbf{C} = \mathbf{E}\mathbf{C}

where \mathbf{H} is the Hamiltonian matrix, \mathbf{C} is a matrix of coefficients and \mathbf{E} is a diagonal matrix of energies (or ‘eigenvalues’). \mathbf{H} contains matrix elements of (17) with the basis functions of equation (23). \mathbf{C} is a matrix of (unknown) coefficients which multiply each basis function of equation (23) to give a variational approximation to the eigenfunction of that rotational-vibrational state. Each column will give the coefficients required for a single state. E contains the energies of each state. Equation (24) is an eigenvalue equation. To solve it the Hamiltonian matrix is ‘diagonalised’. This is a standard problem in many areas of science and mathematics and general programs have been written for its solution. TROVE uses the LAPACK/BLAS libraries. The full Hamiltonian decouples into blocks of independent J and symmetry \Gamma that is, matrix elements between different J and \Gamma are zero. This greatly reduces the size of the matrices to be diagonalised.

After diagonalisation of \mathbf{H} the coefficients are stored (if verb|Eigenfunc SAVE| is used). Further calculations using the eigenfunctions (for example, obtaining transition intensities) are then simplified into multiplying and adding the corresponding coefficients together and multiplying pre-computed integrals.

Symmetrised Basis Functions in TROVE

Symmetry plays a crucial part in the TROVE program and the calculation of molecular energy levels and spectra in general. Using symmetry systematically via the application of Group Theory can greatly reduce the effort required to solve the Schrödinger equation as many of the required matrix elements which are zero can be shown to be so without computing them explicitly. Symmetry is also required to assess which spectroscopic transitions are possible [98BuJe].

TROVE implements symmetry methods in a numerical manner. The following section is based on a recent paper by Yurchenko, Yachmenev and Ovsyannikov [17YuYaOv] which discusses TROVE’s implementation of symmetry in a pedagogical manner with examples. The reader is referred there for more detail and only a summary is given here.

Following the symmetry paper the rotational-vibrational basis functions of equation (23) are written as

(25)\Phi_{k,\nu}^J(\theta,\phi,\chi,\xi_1,\xi_2\cdots, \xi_{3N-6}) = \prod_{v} |\nu_v \rangle \times |J,K,m,\pm \rangle.

Symmetry adapted basis functions are formed from linear combinations of these primitive functions as

(26)\Psi_{\mu,n}^{J,\Gamma_s} = \sum_{k,v} T_{k,v,n}^{\mu,J,\Gamma_s} \Phi_{k,\nu}^J.

In this equation the T_{k,v,n}^{\mu,J,\Gamma_s} are symmetrization coefficients (not to be confused with the variational expansion coefficients of equation (24). Here \mu is a counting number, \Gamma_s is symmetry label of a certain irreducible representation (irrep) of the symmetry group (see Atkin’s MQM for a good introduction to this) and n is used for degenerate symmetries.

Symmetrised basis functions have the important advantage that they the make the Hamiltonian block diagonal. That is

(27)\left< \Psi_{\mu,n}^{J,\Gamma_s} | H^{rv} | \Psi_{\mu',n'}^{J,\Gamma_t} \right> = H_{\mu,\mu'} \delta_{s,t}\delta_{n,n'}

so that each J_{\Gamma_s,n} Hamiltonian block can be diagonalised independently. This gives a huge time and memory saving, especially for large basis sets and allows the calculation of different symmetries to be carried out in parallel. It also means that J, \Gamma_s (and n a symmetry label for degenerate states) can be considered ‘good’ quantum numbers for labelling states. With the advantage of symmetrised functions noted, the method for obtaining them used in TROVE will be described.

The Hamiltonian operator for a system \hat{H} commutes with all operations of a given symmetry operation R

(28)\left[\hat{H},R\right] = 0

and eigenfunctions of \hat{H} are also eigenfunctions of R (as a simple example of this, a hydrogen s-orbital is invariant under all operations of the spherical group R^3). This means that the eigenfunctions transform as an irrep of the symmetry group, \mathbf{G}.

The full rovibrational Hamiltonian H^{rv} is not used to find symmetrised functions since this is exactly the process we are trying to simplify. Instead a set of reduced Hamiltonians \hat{H}^{(i)} is introduced, similar to what was done for finding 1D basis functions in equation (19). The approach used in TROVE for this is as follows:

  1. All ro-vibrational degrees of freedom are divided into L symmetrically independent subspaces which form subgroups of \mathbf{G}. For example in the PF3 example from chapter Theory, the basis block was divided into ‘1s’ and ‘2s’ for the stretches and bends respectively.

  2. For each subspace i = 1, \cdots, L, a reduced Hamiltonian operator \hat{H}^{(i)} is constructed by neglecting or integrating over the other degrees of freedom.

  3. The symmetry-adapted wave functions for each subspace are obtained by diagonalising the corresponding \hat{H}^{(i)}.

  4. The total basis set is built as a direct product of the subspace bases and transformed to irreps using standard approaches.

Symmetrically independent subspaces of coordinates are chosen such that each subspace contains only coordinates which can be symmetrically related by operations of the symmetry group (for example the three stretches of PF3 for one subspace and the three bends as the other).

The details of the above steps are as follows. For each subspace a reduced eigenvalue problem is given by

(29)\hat{H}^{(i)}(\mathbf{Q}^{(i)})\Psi^{(i)}_{\lambda_i}(\mathbf{Q}^{(i)}) = E_{\lambda_i}\Psi^{(i)}_{\lambda_i}(\mathbf{Q}^{(i)})

where \mathbf{Q}^{(i)} is a set of coordinates (\xi_1,\xi_2,\cdots) from a subspace i and \lambda_i is a counter of each solution from i. The eigenfunctions will transform as an irrpe of the molecular symmetry group \mathbf{G}. The reduced Hamiltonian is constructed by averaging the total vibrational (J=0) Hamiltonian \hat{H} on the ground-state primitive vibrational basis functions of the other subspaces

(30)\hat{H}^{(i)}(\mathbf{Q}^{(i)}) = \left< 0_p| \langle 0_q | \cdots \left<0_r|\hat{H}|0_r \right> \cdots |0_q \rangle |0_p \right>

As well as giving symmetrised functions, solving equation (29) also gives better basis functions for the system since the problem is closer to the full dimensionality. The solutions can also be contracted, by energy for example. The TROVE symmetry paper gives examples of how the method works for AB2 and XY3 type molecules. The total basis set for the full dimensionality of the molecule is constructed by a direct product of the L symmetrised basis sets. This is then transformed to irreps using standard approaches.

Although the solutions of the reduced Schrödinger equations are guaranteed to be an irrep of the symmetry group \mathbf{G} it may not be obvious to which symmetry a given function belongs. Degenerate solutions will also be mixed together. TROVE solves both of these problems in a numerical manner. To determine which irrep a given solutions belongs to, TROVE samples the basis functions on a grid of geometries N^{(i)}_{\text{grid}}. The number of these points used is the value of verb|sample_points| in the TROVE input file. For a given subspace i, a random grid of geometries of that space \mathbf{Q}_k^{(i)} (k=1,\cdots,N^{(i)}_{\text{grid}}), all symmetry related images R (\mathbf{Q}^{(i)}) are generated. These are used to find the values of the wave functions \Psi^{(i)}_{\lambda_i}(R \mathbf{Q}^{(i)}) at each geometry. This allows the transformation matrices \mathbf{D}[R] for each operation of the group \mathbf{G} to be established and the symmetry of wave functions to be worked out.

The same procedure is used to obtained symmetrised functions for J>0 rotational-vibrational states.

The J=0 Contraction Method

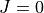The basis functions described in section sec.rot_basis which are a product of rigid-rotor and primitive (or symmetry-adapted) basis functions can in principle be used for J>0 calculations. This approach requires the full Hamiltonian matrix for each symmetry to be diagonalised each time and ignores the fact that the purely vibrational J=0 problem has already been solved. A better approach is to use the 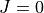J=0 vibrational solutions as a basis for J>0 calculations. 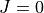This is the J=0 contraction.

The 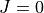J=0 vibrational eigenfunctions \Psi_{J=0,i}^{\Gamma_s} for each symmetry \Gamma_s of the molecule is first obtained by diagonalising the vibrational Hamiltonian. These are then multiplied by the rigid rotor functions discussed in section sec.rot_basis and symmetrised. This gives a basis \Psi^{\Gamma_s}_{J,K,i}.

The Hamiltonian is given as

(31)\hat{T} = \frac{1}{2} \sum_{\alpha,\alpha'} \hat{J}_{\alpha} G_{\alpha,\alpha'}(\xi) \hat{J}_{\alpha'} -\frac{i \hbar}{2} \sum_{\alpha,n} \left[\hat{J}_{\alpha} G_{\alpha,n}(\xi) \frac{\partial}{\partial \xi_n} + \frac{\partial}{\partial \xi_n} G_{\alpha,n}(\xi) \hat{J}_{\alpha} \right] +\hat{H}_{\text{vib}}

where the centre of mass motion has been ignored and simplified notation used. Here \hat{H}_{\text{vib}} is given as

(32)\hat{H}_{\text{vib}} = -\frac{\hbar^2}{2} \sum_{n,n'} \frac{\partial}{\partial \xi_n} G_{n,n'}(\xi) \frac{\partial}{\partial \xi_{n'}} + U(\xi) + V.

The functions \Psi_{J=0,i}^{\Gamma_s} are solutions for this Hamiltonian and satisfy

(33)\left< \Psi_{J=0,i}^{\Gamma_s} | \hat{H}_{\text{vib}} | \Psi_{J=0,i'}^{\Gamma_s} \right> = E_i^{\text{vib}} \delta_{i,i'}.

Calculating matrix elements of the Hamiltonian equation (31) can be further simplified by pre-computing integrals using the 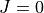J=0 basis

G_{\alpha,\alpha'}^{\Gamma_s,\Gamma_s',i,i'} = \left< \Psi_{J=0,i}^{\Gamma_s} | G_{\alpha,\alpha'} | \Psi_{J=0,i'}^{\Gamma_s'} \right>

and

G_{\alpha,n}^{\Gamma_s,\Gamma_s',i,i'} = \left< \Psi_{J=0,i}^{\Gamma_s} | \left[\hat{J}_{\alpha} G_{\alpha,n}(\xi) \frac{\partial}{\partial \xi_n} + \frac{\partial}{\partial \xi_n} G_{\alpha,n}(\xi) \hat{J}_{\alpha} \right] \Psi_{J=0,i'}^{\Gamma_s'} \right>.

Matrix elements are neglected if the values are below a certain tolerance, usually 10^{-16}. This is the last step where the primitive basis set is required. Many of the matrix elements involving the rigid-rotor functions are analytic.

The 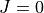J=0 contraction greatly speeds up the calculation of J>0 matrix elements. Matrix elements of the dipole moment surface can also be calculated using a similar approach.

Another feature of this approach is the possibility to use experimental band centres in equation (33) instead of calculated vibrational energies. This is denoted the ‘empirical basis set correction’ since effectively the vibrational basis set is improved (there is no correction to the rotational structure using this method). This is a useful and pragmatic approach when many experimental energies are available, especially if the band of interest has a Q-branch. Even after refinement some bands may not agree satisfactorily and so can be corrected using this method. In TROVE this is implemented by changing the values in the j0descr.chk files.

Intensity Calculations in TROVE

Transition intensities can be calculated using TROVE but for the production of line lists, the GAIN program is recommended. To calculate intensities a dipole moment surface (DMS) for the molecule of interest is required. This is similar to a PES but instead of giving the molecule’s electronic energy as a function of molecular geometry, it gives a molecule’s dipole. Since this is a vector quantity a DMS has three values associated with a given molecular geometry: one for each X,Y,Z coordinate.

Similar to the PES, TROVE expands the DMS in terms of internal coordinates of the molecule to a given expansion order chosen by the user. Matrix elements of the DMS between basis functions are computed in TROVE and can also be converted to the 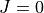J=0 contraction scheme for use in J>0 calculations. The pre-computation of these matrix elements allows for faster computation of transition intensities involving eigenfunction of each ro-vibrational state.

The Einstein-A coefficient for a particular transition from the initial state i to the final state f is given by

(34)A_{if} = \frac{8 \pi^4 \nu^3_{if}}{3h} (2J_i + 1) \sum_{\alpha = x, y, z} \left| \langle \Psi^f \bar{\mu}_{\alpha} {\Psi^i}\rangle \right|^2

where J_i is the rotation quantum number for the initial state, h is Planck’s constant, \nu_{if} is the transition frequency (hc \cdot \nu_{if} = E_f - E_i) and \Psi^f and \Psi^i are the initial and final rovibrational states respectively. Since matrix elements of the dipole between states are pre-computed by TROVE this integral becomes a sum of terms. Technical details of how these integrals are evaluated is given in the GAIN paper [GAIN].

The Einstein-A coefficients are costly to compute but note that they are temperature independent. Once computed for transitions between all states of interest (usually to some value of J), the transition intensities (and spectra) for any temperature can be computed relatively straightforwardly (using Exocross [Exocross] for example).

The absolute absorption intensities are given by

(35)I(f \leftarrow i) = \frac{A_{if}}{8 \pi c} g_{ns} (2 J_f + 1) \frac{\exp(-E_i/kT) }{Q(T) \nu^2_{if}}\times \left[ 1 - \exp\left( - \frac{c_2 \nu_{if}}{T}\right)\right]

where k is the Boltzmann constant, T is the absolute temperature, Q(T) is the partition function, g_{ns} is the nuclear statistical weight and c_2 = hc/k.