Quantum numbers¶

Largest basis set contribution approach¶

The main concept behind assigning vibrational quantum numbers is to compare vibrational eigenfunctions $\psi_{i}$ (or corresponding densities $|\psi_i|^2$ ) to and associate with some reference wavefunctions with well defined quantum numbers, e.g. basis functions. TROVE uses the largest coefficient approach from the expansion of eigenvectors in terms of the basis functions. Consider, for example, variationally computed wavefunctions of the form

(1)¶ $\psi_{i} = \sum_{v_1,v_2,\ldots} C_{v_1,v_2,\ldots,}^{i} \phi_{v_1,v_2,\ldots v_M}.$

An eigen-state $\psi_{i}$ is said to inherit quantum numbers $v_1', v'_2,\ldots, v'_M$ of the most ‘similar’ basis function $\phi_{v'_1,v_2',v'_3\ldots v'_M}$ . According to the largest contribution concept used in TROVE, the eigen-state $\psi_i$ is assigned the excitation numbers $v'_1, v'_2, \ldots v'_M$ that correspond to the largest basis set contribution measured by the corresponding expansion (eigen-)coefficient $|C_{v'_1,v'_2,\ldots,}^{i}|^2$ . The accuracy of this approach depends on the quality of the basis set and can only provide meaningful information when the coupling between different basis set components is relatively small, i.e. when the magnitude of the largest coefficients $|C_{v'_1,v'_2,\ldots,}^{i}|^2$ is well separated from other contributions. The magnitude of the largest coefficient plays a role of a similarity index between the TROVE eigenfunction and the corresponding reference (basis) function.

1D Primitive basis set¶

The primitive basis functions can be either numerically generated by solving the corresponding Schrödinger equation (e.g. variationally or using the Numerov method) or one of the established orthogonal basis sets, such as Harmonic oscillators. In the latter case, the basis functions as given the corresponding excitation index:

$\phi_{n}(x) = H_{n}(x) e^{-\omega x^2}$

where $H_n(x)$ is a Hermite polynomial. For the numerically generated basis functions obtained variationally, TROVE uses the largest contribution approach described above to assign quantum numbers to the basis functions. For the basis functions obtained using the Numerov-Cooley approach, the excitation indexes of the corresponding 1D wavefunctions are estimated by counting the nodes.

Assignment of the ‘contracted’ symmetry adapted basis functions¶

Following the TROVE pipeline of step 1, after the 1D primitive basis functions are contracted, TROVE solves reduced Hamiltonians for a set of sub-classes with the goal of building a symmetry adapted contracted basis set. These reduced problems are solved variationally and therefore the corresponding eigen-functions can be assigned the quantum numbers using the largest contribution approach. Here TROVE uses its native quantum numbers that directly correspond to the basis set as defined in the section BASIS. For example, or a symmetric triatomic molecule of the type XY₂, a typical Basis set is defined as follows

BASIS
 0,'JKtau', Jrot 0
 1,'numerov','linear', 'morse', range 0,  4,  resc 1.0, points 600,borders -0.5,1.40
 1,'numerov','linear', 'morse', range 0,  4,  resc 1.0, points 600,borders -0.5,1.40
 2,'numerov','linear', 'linear', range 0, 4,  resc 1.0, points 4000,borders   4.0,150.0 deg
END

where the first line corresponds to the rotational basis set (sub-class 0), lines 2 and 3 belong to sub-class 1 containing two stretching modes XY₁ and XY₂. The last line describes the bending mode from sub-class 2. After solving the reduced vibrational problem for class 1, the energies in the TROVE standard output are printed out as given by

Symmetry of the contracted solution, class:   1
     i       ener         deg  symmetry  quanta:
      0.00000000   1   1  A1     0   0   0    0
   2606.33588428   1   1  A1     1   0   0    0
   3289.35032517   1   4  B2     0   1   0    0
   5167.94761210   1   1  A1     1   1   0    0
   5792.74038338   1   4  B2     0   2   0    0
   6500.04075468   1   1  A1     1   1   0    0
   7704.33822743   1   1  A1     2   1   0    0
   8334.12791848   1   4  B2     0   3   0    0
   9079.13120953   1   1  A1     0   3   0    0
   9911.69433846   1   4  B2     1   2   0    0
  10163.09614410   1   1  A1     2   2   0    0
  10789.04196300   1   4  B2     4   0   0    0
  11578.19544716   1   1  A1     4   0   0    0
  12431.56258951   1   4  B2     3   1   0    0
  13239.83629333   1   1  A1     2   2   0    0

where the 1st column (i) is a counting index of the contracted solution for sub-class 1; the 2nd column (ener) contains the energies (in wavenumbers); col 3 (deg) shows the degeneracy of the state (here it is 1 for the C₂v(M) symmetry group), columns 4 and 5 contain the symmetry (irrep), the symmetry index (1,2,3,4) and the symmetry label (A1, A2, B1, B2); cols 6 and 7 are the stretching quantum $v_1,v_2$ ; col 8 gives bending quantum number (here it is zero for the stretching sub-class) and the last column is reserved for the rotational quantum number of sub-class 0 (not used in practice for the vibrational basis sets).

The exact distribution of the tow quanta between the two equivalent stretching modes $v_1,v_2$ is random, only the total quanta $v_1+v_2$ has a physical meaning plus the total symmetry. Using these two criteria it is usually possible to match the TROVE (local mode) quantum numbers to the spectroscopic (normal mode) quantum numbers. Form example, the energy state 2 ( $E_2 = 2606.33588428$ cm^-1) is assigned (1,0) A1, which is the (1,0,0) state in the normal mode notation. The next energy state 3 ( $E_2 = 3289.35032517$ cm^-1) is (0,1) B2 has the same total number of quanta (1), but has the symmetry $B_2$ , which corresponds to the (0,0,1) state in the normal mode notation.

The second sub-class in the case of the XY2 molecules is classified as follows:

Symmetry of the contracted solution, class:   2
     i       ener         deg  symmetry  quanta:
      0.00000000   1   1  A1     0   0   0    0
   1186.71845689   1   1  A1     0   0   1    0
   2368.45025285   1   1  A1     0   0   2    0
   3547.01501601   1   1  A1     0   0   3    0
   4728.42983827   1   1  A1     0   0   4    0

with only one active TROVE mode 3 $v_3$ , which is directly mapped to the normal mode states $(0,v_3,0)$ .

Rotational basis set and quantum numbers¶

TROVE uses the rigid rotor wavefunctions $|J,k,m\rangle$ , where $J$ is the total angular momentum in units of $\hbar$ , while $m$ and $k$ are the rotational quantum numbers, describing its projection onto laboratory $Z$ and molecular $z$ -axes, respectively, which satisfy

$m,k = -J,-J-1,\ldots,0,\ldots,J-1,J.$

In calculations of ro-vibrational energy, $m$ plays no direct role and can be ignored. The $k$ quantum number is however a critical quantity, defined by the choice of the $z$ -axes. For asymmetric tops, it is common in spectroscopic applications to choose $z$ along the axis with the smallest moment of inertia, such as frames R-RHO-Z or R-ALPHA-Z used for quasi-linear XY:sun:`2` molecules. For symmetric tops, the $z$ axis is taken as the symmetry axis, such as the R-ALPHA and R-S-DELTA frames used for the XY₃ type. The spherical top XY₄ will be discussed separately.

TROVE uses symmetry adapted rotational basis functions. For asymmetric and symmetric tops, these are the so-called Wang functions $|J,K,\tau\rangle$ ), which are given by

(2)¶ $\begin{split} &|J,0,\tau\rangle = |J,0\rangle, \quad \tau = J\; \hbox{mod}\; 2 , \\ &|J,K,\tau=0\rangle = \frac{1}{\sqrt{2}} \left[ |J,K,m\rangle + (-1)^{J+K} |J,-K,m\rangle \right],\\ &|J,K,\tau=1\rangle = \frac{i (-1)^{\sigma} }{\sqrt{2}} \left[ |J,K,m\rangle - (-1)^{J+K} |J,-K,m\rangle \right]. \end{split}$

Here $K=|k|$ , $\tau_{\rm rot}$ is the value associated with the parity of $|J,K,\tau_{\rm rot}\rangle$ and $m$ is omitted on the left-hand side for simplicity’s sake. The meaning of $\sigma$ is explained below. $K$ is commonly used as the rotational quantum number, $K_a$ or $K_c$ , depending on the orientation of the $z$ axis. The sign of $k$ is, however, not a physically meaningful quantity of a rotational eigen-state, but the parity $\tau_{\rm rot}$ is.

The $|J,K,\tau\rangle$ functions allow one to classify them according with the corresponding molecular symmetry group they belong to. This is done by following the symmetry properties of the rigid rotor wavefunctions upon the group transformations. For example, the XY₂ Wang functions transform as irreps $\Gamma = A_1, A_2, B_1, B_2$ of the C_{2v`(M) group (:math`Kne 0}), which are defined by the quantum numbers $J, K, \tau$ as follows

$K$	$\tau$	$\Gamma$		$K$	$\tau$	$\Gamma$
even	0	$A_1$		odd	0	$B_2$
even	1	$B_1$		odd	1	$A_2$

As in the case of the vibrational quantum numbers, the rotational components of the ro-vibrational eigenstates are also assigned using the largest contribution approach. Hence, the rotational quantum numbers are

$J$ : the total angular momentum rotational quantum number;

$K$ : the projection of $J$ on the molecular axis $z$ rotational quantum number;

$\tau$ : a rotational index defining the state parity;

$\Gamma_{\rm rot}$ : the rotational symmetry.

Due to symmetry $\Gamma$ , the parity $\tau$ is in fact redundant.

The mappings between the $J, K, \tau$ and $\Gamma$ appear in modules mol_*.f90. For example, for this C_{2v`(M) example of a XY:sub:`2} type molecule the mapping is given by (see mol_xy2.f90):

   !
case('C2V','C2V(M)')
   !
   gamma = 0
   ideg = 1
   if (mod(K+2,2)==0.and.tau==0) gamma = 1
   if (mod(K+2,2)==0.and.tau==1) gamma = 2
   if (mod(K+2,2)/=0.and.tau==0) gamma = 4
   if (mod(K+2,2)/=0.and.tau==1) gamma = 3
   !

The symmetry classification of the rotational basis functions can be also found in the standard TROVE output:

Symmetry of the contracted solution, class:   0
     i       ener         deg  symmetry  j   k  tau  quanta:
    151.97406555   1   1  A1     4   0   0   0   0   0
    153.39155239   1   4  B2     4   1   0   0   0   0
    153.39155239   1   3  B1     4   1   1   0   0   0
    157.64401293   1   1  A1     4   2   0   0   0   0
    157.64401293   1   2  A2     4   2   1   0   0   0
    164.73144716   1   4  B2     4   3   0   0   0   0
    164.73144716   1   3  B1     4   3   1   0   0   0
    174.65385507   1   1  A1     4   4   0   0   0   0
    174.65385507   1   2  A2     4   4   1   0   0   0

where class: 0 corresponds to the rotational sub-set = 0.

T_d symmetry¶

The Wang-functions cannot be used for symmetry adaptation of the T_d rotational basis. This is because the group symmetry transformations cannot be associated with equivalent rotations about the $x$ , $y$ or $z$ axes only. As a result, symmetry-adapted rotational functions are obtained as a general linear combinations of $|J,k,m\rangle$ with $k$ spanning all $k=-J\ldots J$ . Because of that, the rotational quantum number $K$ can no longer be used for classification of the symmetrised rigid-rotor combinations. Instead they are labelled as $|J,\Gamma,n\rangle$ , where $\Gamma$ is the symmetry and $n$ is a counting index:

(3)¶ $|J,\Gamma,n\rangle = \sum_{k} T_{n,k}^{(J,\Gamma)} | J,k,m\rangle.$

Assignment of the ro-vibrational eigen-functions¶

Once the individual vibrational basis set components are defined together with their quantum number classifications, the (ro-)vibrational basis set is constructed as a direct product of its components. The latter inherits the quantum numbers of the individual components to form the assignment of the (ro-)vibrational basis functions. For example, by combining

$\begin{split} \phi_{v_1,v_2}^{\Gamma_{\rm str}}(r_1,r_2) &= | v_1, v_2, \Gamma_{\rm str} \rangle,\\ \phi_{v_3}^{\Gamma_{\rm bend}}(\alpha) &= | v_3, \Gamma_{\rm bend} \rangle,\\ \phi_{J,K,\Gamma_{\rm rot}}(\phi,\theta,\chi) &= | J,K,\Gamma_{\rm rot} \rangle, \\ \end{split}$

a ro-vibrational basis function :math`phi_{J,K,v_1,v_2,v_3,Gamma_{rm tot}}` is formed as a symmetrised combination:

$\phi_{J,K,v_1,v_2,v_3,\Gamma_{\rm tot}} = \{| v_1, v_2, \Gamma_{\rm str} \otimes | v_3, \Gamma_{\rm bend} \rangle \otimes | J,K,\Gamma_{\rm rot} \rangle \}^{\Gamma_{\rm tot}}$

The ro-vibrational eigenfunctions are computed variationally on the basis the symmetry adapted basis of $\phi_{J,K,v_1,v_2,v_3,\Gamma_{\rm tot}}$ . The TROVE quantum numbers obtained using the largest contribution approach eigenfunction thus include:

$J$ is the total angular momentum rotational quantum number.

$\Gamma_{\rm tot}$ is the total symmetry (irrep) of the corresponding molecular symmetry group.

$K$ is a rotational quantum number describing the projection of $J$ on the molecular axis $z$ .

$\Gamma_{\rm rot}$ is the rotational symmetry of the corresponding molecular symmetry group.

$v_1, v_2, \ldots$ are the TROVE (local mode) quantum numbers.

$\Gamma_{\rm vib}$ is the vibrational symmetry of the corresponding molecular symmetry group.

TROVE energy output¶

Consider an example of H₂S calculations. The the J=0 energy output for the total symmetry $A_1$ is given by

------ ------ ------------- ------- --- -- --- ---- ----- ---- --- ------ -------- ------ --- --- --- -------- -----
  1        2        3           4    5  6  7    8    9     10   11  12       13      14  15  16  17       18    19
------ ------ ------------- ------- --- -- --- ---- ----- ---- --- ------ -------- ------ --- --- --- -------- -----
G_tot      n     Energy        G_r   J  K  t    Gv1 Gv2     v1  v2  v3       C_i      n1  n2  n3  l    ivib1   ivib2
------ ------ ------------- ------- --- -- --- ---- ----- ---- --- ------ -------- ------ --- --- --- -------- -----
 A1        1      0.000000   ( A1 ;  0  0  0 ) ( A1  A1 ;   0   0   0 )      1.00 (   0   0   0   0 ) (    1    1 )
 A1        2   1172.667646   ( A1 ;  0  0  0 ) ( A1  A1 ;   0   0   1 )      1.00 (   0   0   1   0 ) (    1    2 )
 A1        3   2335.297519   ( A1 ;  0  0  0 ) ( A1  A1 ;   0   0   2 )      0.98 (   0   0   2   0 ) (    1    3 )
 A1        4   2608.713940   ( A1 ;  0  0  0 ) ( A1  A1 ;   1   0   0 )      0.99 (   1   0   0   0 ) (    2    1 )
 A1        5   3503.042415   ( A1 ;  0  0  0 ) ( A1  A1 ;   0   0   3 )      0.95 (   0   0   3   0 ) (    1    4 )
 A1        6   3765.459944   ( A1 ;  0  0  0 ) ( A1  A1 ;   1   0   1 )      0.95 (   1   0   1   0 ) (    2    2 )
 A1        7   4675.006191   ( A1 ;  0  0  0 ) ( A1  A1 ;   0   0   4 )      0.92 (   0   0   4   0 ) (    1    5 )
 ...........
 ...........

where the designation of the columns is as follows

Col 1: G_tot is the total symmetry of a ro-vibrational state;

Col 2: n is the counting number of the energy;

Col 3: Energy term value of the state;

Col 4: G_r is the rotational symmetry;

Col 5: J is the total angular momentum rotational quantum number;

Col 6: k is a rotational quantum number (projection of $J$ on the molecular axis $z$ );

Col 7: t is a rotational index defining the state parity $\tau$ ;

Col 8-9: Gv1 are Gv2 are the vibrational symmetries of the corresponding vibrational sub-classes;

Cols 10-12: v1, v2, v3 are the TROVE (local mode) vibrational quantum numbers;

Col 13: C_i is the largest eigen-coefficient used in the assignment.

Cols 14-17: K, n1, n2, n3 are placeholder for the user-defined quantum numbers to be propagated to the final ro-vibrational eigenstates.

Cols 18-19: ivib1, ivib2 are the counting indices of sub-classes in the representation of direct products of the symmetry adapted ‘contracted’ basis set.

It should be noted that for equivalent modes, such as the two stretches in the case of H₂S, only their total quanta $v_1+v_2$ is meaningful, not the individual values. For example, the following TROVE stretching states $(v_1,v_2) = (2,0), (1,1)$ , and $(0,2)$ ( $v_1+v+2 = 2$ ) are equivalent and cannot be distinguished without some extra information (e.g. their symmetry).

Similarity, the $B_2$ symmetry TROVE output is given by

Variational solution - irreducible representation
  Gamma     i       value             j  k  t   quanta
  B2        1   3280.145078   ( A1 ;  0  0  0 ) ( B2  A1 ;   0   1   0 )      1.00 (   1   0   0   0 ) (    3    1 )
  B2        2   4415.876421   ( A1 ;  0  0  0 ) ( B2  A1 ;   0   1   1 )      0.99 (   1   0   1   0 ) (    3    2 )
  B2        3   5556.806722   ( A1 ;  0  0  0 ) ( B2  A1 ;   0   1   2 )      0.97 (   1   0   2   0 ) (    3    3 )
  B2        4   5785.428853   ( A1 ;  0  0  0 ) ( B2  A1 ;   0   2   0 )      0.99 (   2   0   0   0 ) (    5    1 )
  B2        5   6717.570020   ( A1 ;  0  0  0 ) ( B2  A1 ;   0   1   3 )      0.96 (   1   0   3   0 ) (    3    4 )
  B2        6   6914.548146   ( A1 ;  0  0  0 ) ( B2  A1 ;   0   2   1 )      0.96 (   2   0   1   0 ) (    5    2 )
  B2        7   8041.707663   ( A1 ;  0  0  0 ) ( B2  A1 ;   0   2   2 )      0.98 (   2   0   2   0 ) (    5    3 )
  ....

The non-rigourous quantum numbers $K$ and $v_i$ are defined using the largest eigen-coefficient approach and are approximate. They represent the measure of how the given wavefunction is similar to a single selected basis set function selected as the largest contribution the corresponding expansion. The quality of the assignment can be judged based on the expansion eigen-coefficients (column with numbers $\le 1$ and two decimal points): coefficients smaller than 0.7 indicate that the corresponding quantum number are less reliable. Due to this approximate nature of the TROVE quantum numbers, the TROVE assignment is usually not complete and unambiguous. It is common to find states with duplicate assignments as well as some missing combinations (see Quantum Numbers).

In order to help resolve ensuing ambiguity and degeneracies, the quantum numbers from the second largest contribution can be printed. This feature can be activated using the NASSIGNMENTS keyword as part of the PRINT section. The section can appear anywhere in main body of the input file, for example:

DIAGONALIZER
 SYEV
 enermax 20000
end

print
 Nassignments  2
end

Quantum numbers in the 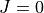$J=0$ representation¶

The ro-vibrational calculations in the 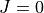$J=0$ representation (step 3) are characterised by a single contracted 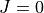$J=0$ sub-class with the basis set given by

$\phi_{J,K,v_1,v_2,v_3, \ldots \Gamma_{\rm tot}} = \{| v_1, v_2, v_3, \ldots \Gamma_{\rm vib} \rangle \otimes | J,K,\Gamma_{\rm rot} \rangle \}^{\Gamma_{\rm tot}}$

Phi_{lambda}^{(J=0)} |J,K,taurangle,

where :math`| J,K,Gamma_{rm rot} rangle ` is a rigid rotor basis function. Therefore, in this case the energy output has a slightly different form:

------ ------ ------------- ------- --- -- --- ----- ----- --- ----   -------- ------ --- --- --- --------
  1        2        3           4    5  6  7     8      9  10   11       12       13   14 15  16       17
------ ------ ------------- ------- --- -- --- ----- ----- --- ----   -------- ----- --- --- ---- --------
G_tot      n     Energy        G_r   J  K  t     Gv    v1  v2  v3        C_i     n1   n2  n3  l      ivib
------ ------ ------------- ------- --- -- --- ----- ----- --- ----   -------- ----- --- --- ---- --------
 A1        1   3329.579210   ( B2 ;  1  1  0 ) ( B2 ;   0   1   0 )      1.00 (   1   0   0   0 ) (    5 )
 A1        2   4465.843673   ( B2 ;  1  1  0 ) ( B2 ;   0   1   1 )      1.00 (   1   0   1   0 ) (    8 )
 A1        3   5607.333481   ( B2 ;  1  1  0 ) ( B2 ;   0   1   2 )      1.00 (   1   0   2   0 ) (   12 )
 A1        4   5834.782843   ( B2 ;  1  1  0 ) ( B2 ;   0   2   0 )      1.00 (   2   0   0   0 ) (   13 )
 A1        5   6770.421491   ( B2 ;  1  1  0 ) ( B2 ;   0   1   3 )      1.00 (   1   0   3   0 ) (   17 )
 A1        6   6964.556323   ( B2 ;  1  1  0 ) ( B2 ;   0   2   1 )      1.00 (   2   0   1   0 ) (   18 )

where

Col 8: Gv is now a single vibrational symmetry

Col 17: ivib is a single counting index of the vibrational symmetry adapted ‘contracted’ basis set.

In fact, ivib is an unique vibrational ID and can be used to track the vibrational quantum numbers through the ro-vibrational calculations.

‘Normal mode’ quantum numbers¶

It is common for spectroscopic applications to relate the vibrational assignment to normal mode quantum numbers with the associated harmonic normal mode wavefunctions. Correlating TROVE local mode quantum numbers to the normal mode ones is not always trivial. Consider the above H₂S example. The normal mode quantum numbers for this C_2v(M) molecule are $(n_1,n_2,n_3)$ , where $n_1$ represents a symmetric stretch ( $A_1$ ), $n_2$ is a symmetric bend ( $A_1$ ) and $n_3$ an asymmetric stretch ( $B_2$ ). In the corresponding TROVE quantum numbers scheme $(v_1,v_2,v_3)$ , $v_1,v_2$ are two equivalent local mode stretches (un-symmetrised) and $v_3$ is a bending quantum number.

It is trivial to assign normal mode quantum numbers $(n_1,n_2,n_3)$ to the following lowest 5 vibrational states based on their quanta and symmetries:

G_tot	n	Energy	v1	v2	v3	n1	n2	n3
A1	1	0.000000	0	0	0	0	0	0
A1	2	1172.667646	0	0	1	0	1	0
A1	3	2335.297519	0	0	2	0	2	0
A1	4	2608.713940	1	0	0	1	0	0
B2	5	3280.145078	0	1	0	0	0	1

Indeed, all the pure bending TROVE quantum numbers $(0,0,v_3)$ can be directly mapped to the normal mode quantum numbers $(0,v_2,0)$ . For the stretching modes, although only the sum of the TROVE quantum numbers $v_1+v_2$ is unambiguous, the correlation to the normal modes can be established with the help of the symmetry: $v_1+v_2=1, A_1$ is $(n_1,n_2,n_3) = (1,0,0)$ and $v_1+v_2=1, B_2$ is $(n_1,n_2,n_3) = (0,0,1)$ .

It is less trivial for higher excitations, where knowing the symmetry $A_1, B_2$ of different stretching combinations corresponding to the same value of $v_1+v_2$ is not enough to resolve the ambiguity. What helps in this case is to notice that the energy quanta of the $n_1$ stretching component is lower than that of $n_3$ . Combining this assumption with the state symmetry allows one to correlate the TROVE and normal model quantum numbers to the other vibrational states as given by

G_tot

n

Energy

v1

v2

v3

n1

n2

n3

A1

6

3503.042415

0

0

3

0

3

0

A1

7

3765.459944

1

0

1

1

1

0

B2

8

4415.876421

0

1

1

0

1

1

A1

9

4675.006191

0

0

4

0

4

0

A1

10

4927.853585

1

0

1

1

2

0

A1

11

5171.458835

1

1

0

2

0

0

B2

12

5556.806722

0

1

2

0

2

1

B2

13

5785.428853

0

2

0

1

0

1

A1

14

6063.870902

1

0

3

1

3

0

A1

15

6318.807464

1

1

1

2

1

0

B2

16

6717.570020

0

1

3

0

3

1

B2

17

6914.548146

0

2

1

1

1

1

It is however less trivial to use this approach for rotationally excited states $(J>0)$ , for larger number of sub-states and for degenerate symmetries. In the following chapter, we show, how the checkpoint file contr_descr.chk can be used to map the TROVE quantum numbers to the normal mode ones at the sub-class level and then propagate them to any the ro-vibrational state.

Assigning ‘normal mode’ quantum numbers¶

Considering that different vibrational and rotational contributions can be heavily mixed in the final ro-vibrational eigen-vectors, correlating the TROVE and spectroscopic (‘normal mode’) quantum numbers (QN) can be challenging. It is therefore instructive to start correlating them as earlier in calculation pipeline as possible. The earliest stage when this can be sensibly done is for the symmetry adapted reduced contractions. The correlation is not a straightforward procedure, currently requiring a human to build a mapping between the TROVE local mode and normal mode representation. The propagation of this mapping is done via a QN placeholder in the descr checkpoint files.

Consider for example the local $(v_1,v_2,v_3)$ to normal $(n_1,n_2,n_3)$ mode mapping presented above for the H₂S example. Using this correlation, we can modify the QN placeholder section in the contr_descr.chk file as follows:

Class #       1
            15            15  <-  number of roots and dimension of basis

                                                 ---- --- ---      --- ---- ---
                                                  v1  v2  v3        n1  n2  n3
                                                 ---- --- ---      --- ---- ---
      1   1       1   1   3631.457962557469   0   0   0   0     0   0   0   0         0.99650855
      2   1       2   1   6237.793846833702   0   0   1   0     0   1   0   0        -0.70449312
      3   4       3   1   6920.808287732268   0   1   0   0     0   0   0   1         0.69933488
      4   1       4   1   8799.405574657821   0   1   1   0     0   2   0   0        -0.66971512
      5   4       5   1   9424.198345933786   0   0   2   0     0   1   0   1         0.69495690
      6   1       6   1  10131.498717237881   0   1   1   0     0   0   0   2         0.72224834
      7   1       7   1  11335.796189988205   0   2   1   0     0   3   0   0        -0.57998640
      8   4       8   1  11965.585881042271   0   0   3   0     0   2   0   1         0.62572431
      9   1       9   1  12710.589172085258   0   3   0   0     0   1   0   2        -0.55924495
     10   4      10   1  13543.152301015232   0   1   2   0     0   0   0   3         0.61849364
     11   1      11   1  13794.554106652784   0   2   2   0     0   4   0   0         0.55571833
     12   4      12   1  14420.499925557249   0   4   0   0     0   3   0   1         0.55493771
     13   1      13   1  15209.653409713983   0   4   0   0     0   2   0   2         0.58837860
     14   4      14   1  16063.020552071870   0   1   3   0     0   1   0   3         0.54684816
     15   1      15   1  16871.294255882527   0   2   2   0     0   0   0   4         0.65892621
Class #       2
             5             5  <-  number of roots and dimension of basis
                                                 ---- --- ---      --- ---- ---
                                                  v1  v2  v3        n1  n2  n3
                                                 ---- --- ---      --- ---- ---
     16   1       1   1   3676.343781669159   0   0   0   0     0   0   0   0         0.99914576
     17   1       2   1   4863.062238559608   0   0   0   1     0   0   1   0        -0.99741510
     18   1       3   1   6044.794034517188   0   0   0   2     0   0   2   0        -0.99558857
     19   1       4   1   7223.358797674689   0   0   0   3     0   0   3   0        -0.99426327
     20   1       5   1   8404.773619941838   0   0   0   4     0   0   4   0         0.99669840
End Quantum numbers and energies

The format of this checkpoint file contr_descr.chk is not sensitive to the number of spaces between the columns, but is sensitive to their order as well as to the order of the lines.

This file can be then read into the TROVE pipeline using the TROVE restart procedure at step 1 by modifying the CHECK_POINT section as follows

CHECK_POINT
 ascii
 kinetic     read
 potential   read
 basis_set   read
 contract    read
 matelem     read    split
 eigenfunc   save
END

Here we assume that all other TROVE components (especially matelem) have been generated. If not, the matelem line can be changed to save. It is important to recompute and store the eigen-vectors (eigenfunc save), which will (re-)generate the eigen_descr*.chk files with the QN template section modified to inherit the normal mode quantum numbers. For our example of H₂S, the energy output is now given by:

Variational solution - irreducible representation
  Gamma     i       value             j  k  t   quanta
  A1        1      0.000000   ( A1 ;  0  0  0 ) ( A1  A1 ;   0   0   0 )      1.00 (   0   0   0   0 ) (    1    1 )
  A1        2   1172.667646   ( A1 ;  0  0  0 ) ( A1  A1 ;   0   0   1 )      1.00 (   0   0   1   0 ) (    1    2 )
  A1        3   2335.297519   ( A1 ;  0  0  0 ) ( A1  A1 ;   0   0   2 )      0.98 (   0   0   2   0 ) (    1    3 )
  A1        4   2608.713940   ( A1 ;  0  0  0 ) ( A1  A1 ;   0   1   0 )      0.99 (   1   0   0   0 ) (    2    1 )
  A1        5   3503.042415   ( A1 ;  0  0  0 ) ( A1  A1 ;   0   0   3 )      0.95 (   0   0   3   0 ) (    1    4 )
  A1        6   3765.459944   ( A1 ;  0  0  0 ) ( A1  A1 ;   0   1   1 )      0.95 (   1   0   1   0 ) (    2    2 )
  A1        7   4675.006191   ( A1 ;  0  0  0 ) ( A1  A1 ;   0   0   4 )      0.92 (   0   0   4   0 ) (    1    5 )
  A1        8   4927.853585   ( A1 ;  0  0  0 ) ( A1  A1 ;   0   1   2 )      0.89 (   1   0   2   0 ) (    2    3 )
  A1        9   5171.458835   ( A1 ;  0  0  0 ) ( A1  A1 ;   1   1   0 )      0.98 (   2   0   0   0 ) (    4    1 )

where the second vibrational QN section now contains the correct normal mode quantum numbers as in the tables above. One can notice that the last QN is kept zero on this case. This field can be useful for an additional quantum number, e.g. the vibrational angular momentum $l$ , required for the linear molecular normal mode classification or in other cases. The normal mode QN are then prorogated to all other energy outputs, including step 3 (ro-vibrational eigenvalues) and step 4 (line list calculations).

Quantum numbers¶

Largest basis set contribution approach¶

1D Primitive basis set¶

Assignment of the ‘contracted’ symmetry adapted basis functions¶

Rotational basis set and quantum numbers¶

T_d symmetry¶

Assignment of the ro-vibrational eigen-functions¶

TROVE energy output¶

Quantum numbers in the $J=0$ representation¶

‘Normal mode’ quantum numbers¶

Assigning ‘normal mode’ quantum numbers¶

Table of Contents

Previous topic

Next topic

This Page

G_tot	n	Energy	v1	v2	v3	n1	n2	n3
A1	6	3503.042415	0	0	3	0	3	0
A1	7	3765.459944	1	0	1	1	1	0
B2	8	4415.876421	0	1	1	0	1	1
A1	9	4675.006191	0	0	4	0	4	0
A1	10	4927.853585	1	0	1	1	2	0
A1	11	5171.458835	1	1	0	2	0	0
B2	12	5556.806722	0	1	2	0	2	1
B2	13	5785.428853	0	2	0	1	0	1
A1	14	6063.870902	1	0	3	1	3	0
A1	15	6318.807464	1	1	1	2	1	0
B2	16	6717.570020	0	1	3	0	3	1
B2	17	6914.548146	0	2	1	1	1	1

Quantum numbers¶

Largest basis set contribution approach¶

1D Primitive basis set¶

Assignment of the ‘contracted’ symmetry adapted basis functions¶

Rotational basis set and quantum numbers¶

Td symmetry¶

Assignment of the ro-vibrational eigen-functions¶

TROVE energy output¶

Quantum numbers in the representation¶

‘Normal mode’ quantum numbers¶

Assigning ‘normal mode’ quantum numbers¶

T_d symmetry¶

Quantum numbers in the $J=0$ representation¶